1、二阶和三阶行列式
二阶行列式
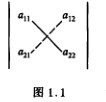
把a11到a22的实联线称为主对角线,a12到a21的虚联线称为副对角线,于是二阶行列式便是主对角线上的两元素之积减去副对角线上的两元素之积所的差。
例如:
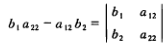
三阶行列式
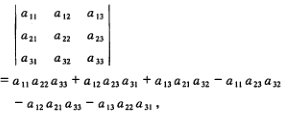

2、全排列及其逆序数
把n个不同的元素排成一列,叫做这n个元素的全排列(排列)。n个不同元素的所有排列的种数,通常用Pn表示。
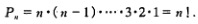
对于n不同的元素,先规定各元素之间有一个标准次序(例如n个不同的自然数,可规定有由小到大为标准次序),于是在这n个元素的任一排列中,当某两个元素的先后次序与标准次序不同时,就说有一个逆序。一个排列中的所有逆序的总数叫做这个排列的逆序数。
逆序数为奇数的排列叫做奇排列,逆序数为偶数的排列叫做偶排列。

3、n阶行列式的定义

4、对换
在排列中,将任意两个元素进行对调,其余的元素不动,这种作出新排列的手续叫做对换。将相邻的元素对换,叫做相邻对换。
定理一:一个排列中的任意的两个元素对换,排列改变奇偶性。

推论:奇排列变成标准排列的对换次数为奇数,偶排列变成标准排列的对换次数为偶数。

定理二:n阶行列式也可定义为:
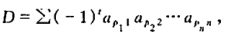
其中t为行标排列的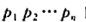 的逆序数。
的逆序数。
5、行列式的性质
